Algemeen
- Netjes werken voorkomt slordigheidsfoutjes.
- Lijnen trek je met potlood en liniaal
- Concentratie is bij cijferen erg belangrijk. Een klein rekenfoutje zorgt ervoor dat de hele som fout is.
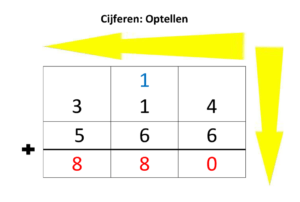
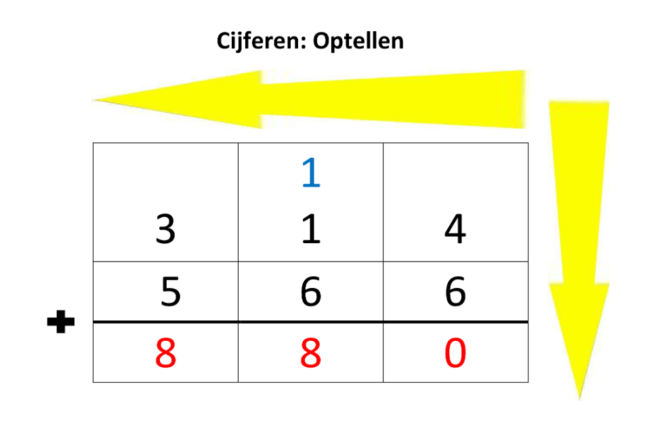
Cijferend optellen
- Zorg ervoor dat alle getallen goed onder elkaar staan (losse onder de losse, tientallen onder de tientallen, enz.).
- Vergeet de cijfers die je moet onthouden niet!
- Soms is het handig om eerst die cijfers bij elkaar te tellen die ‘mooi passen’, die samen een tiental vol maken
(bijvoorbeeld 5+5, 7+3).463
455
555
567Bij bovenstaande optelsom tellen we eerst 463 en 567 bij elkaar op en daarna 455 en 555.
Cijferend aftrekken
Ik moet lenen wanneer het bovenste cijfer kleiner is dan het cijfer dat eraf moet.326
183Bij bovenstaande aftreksom moet er geleend worden bij de 2 van 326.- Pas op met “0-posities”. Wanneer er bij meerdere naast elkaar staande nullen geleend moet worden, wordt de laatste nul een tien en de rest een negen!
- Als ik leen, krijg ik er altijd 10 bij!
- Wordt er bij mij geleend, dan raak ik er 1 kwijt!
Cijferend vermenigvuldigen
- Ken de tafels!!!
- Denk aan het onthouden!!
- Denk bij het eindschema aan het doorstrepen en opschrijven van de nul(len).
- Cijferend X met ‘decimale getallen’ is precies hetzelfde als een X-som zonder kommagetallen. Wel aan het einde van de som de komma op de juiste plek zetten! Die plek vind je door het aantal plaatsen achter de komma te tellen. Doe dit bij beide getallen, tel samen en dan weet je hoeveel cijfers je achter de komma in je antwoord moet hebben!!
Cijferend delen
- Ken de tafels!!!
- Gebruik de schatmethode door mooie, ronde getallen te zoeken die in de buurt liggen (tafels!!!).Bijvoorbeeld: 2376 : 57= 2400 : 60=Voordelen:
Je hebt een stok achter de deur bij het antwoord en je weet hoe groot je beginstap ongeveer moet zijn. - Ken je de volgende nog? Eerst : dan x, dan – en dan aanhalen.
Kun je aanhalen, dan weer van vooraf aan.
Kun je niet meer aanhalen, dan is de som klaar. - Als je na het – werk een uitkomst krijgt die groter is dan de deler, dan weet je dat er iets fout moet zijn!
- Bij het werken met komma’s in de getallen moet je er altijd voor zorgen dat de komma in de deler (VOOR de schuine streep) weggewerkt wordt. Op het moment dat je in zo’n som de komma in het deelgetal (tussen de schuine strepen) tegenkomt, schrijf je de komma ook in het antwoord!!!
Bijvoorbeeld:
3,72/57,3\
———-
372/5730\
Groter dan of kleiner dan
> betekent: is groter dan
< betekent: is kleiner dan
= betekent: is gelijk aan
Kommagetallen
3.462,738
Van bovenstaand getal is:
3: duizendtal
4: honderdtal
6: tiental
2: losse (eenheid)
7: tiende
3: honderdste
8: duizendste
0,123 = honderddrieëntwintig duizendsten
0,73 = drieënzeventig honderdsten
0,5 = vijf tienden
0,5 = een tweede (½)
0,25 = een vierde (¼)
0,75 = drie vierde (¾)
0,125 = 1 achtste
0,1 = één tiende
0,2 = twee tiende
Dagen, maanden, kwartalen…
1 jaar = 12 maanden
1 jaar = 4 kwartalen (1 kwartaal is 3 maanden)
1 jaar = 52 weken
1 jaar = 365 dagen
Een schrikkeljaar heeft 366 dagen (één keer in de vier jaar heeft februari 29 dagen; het jaartal moet te delen zijn door 4!).
De namen van de twaalf maanden:
Januari – 31 dagen
Februari – 28 of 29 dagen
Maart – 31 dagen
Januari, februari en maart vormen samen een kwartaal.
April – 30 dagen
Mei – 31 dagen
Juni – 30 dagen
April, mei en juni vormen samen een kwartaal.
Juli – 31 dagen
Augustus – 31 dagen
September – 30 dagen
Juli, augustus en september vormen samen een kwartaal.
Oktober – 31 dagen
November – 30 dagen
December – 31 dagen
Oktober, november en december vormen samen een kwartaal.
Tip
Wanneer je niet meer zeker weet uit hoeveel dagen een bepaalde maand bestaat, maak dan gebruik van je vuisten:
op een knobbel: 31 dagen
ertussen: 30 dagen
Let op: februari heeft 28 of 29 dagen.
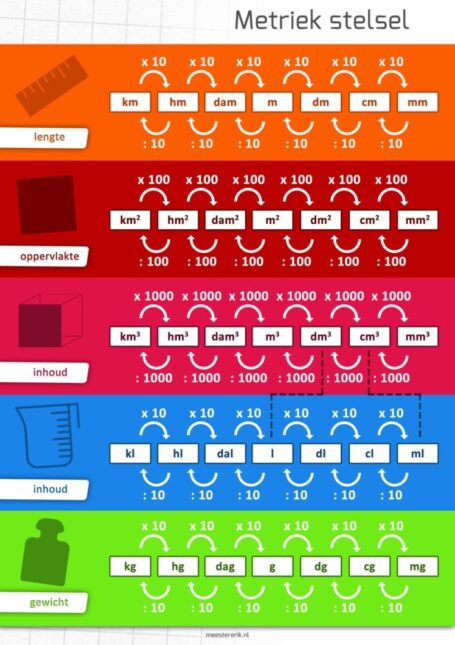
Het metriek stelsel
Afspraak 1
Deze ’trap’ geldt voor: lengtematen, gewichten en liters.
Afspraak 2
Wat gebeurt er nu wanneer ik met oppervlaktematen bezig ben? Dan is iedere stap 2 nullen waard of moet de komma 2 plaatsen verschoven worden.
Afspraak 3
En wat gebeurt er bij inhoudsmaten? Je raadt het al, dan is iedere stap 3 nullen waard of moet de komma 3 plaatsen verschoven worden.
Afspraak 4
Altijd eerst nullen wegwerken, daarna pas met de komma schuiven.
Afspraak 5
| 1 dm3 = 1 liter 1 ha = 1 dam2 1 ca = 1 m2 |
Omtrek, oppervlakte en inhoud
omtrek = lengte + breedte + lengte + breedte
m = meter
oppervlakte = lengte x breedte
m2 = vierkante meter
inhoud = lengte x breedte x hoogte
m3 = kubieke meters
Omtrek
Wanneer ik de omtrek van een figuur wil berekenen, dan wil ik weten welke afstand ik af moet leggen wanneer ik helemaal om het figuur heen loop. Ik meet dan alle afstanden van ieder recht stuk en tel deze afstanden bij elkaar op.
Afspraak 1
Het antwoord geef ik altijd in lengtematen. Bijvoorbeeld: meter (m), centimeter (cm), kilometer (km), enz.
Afspraak 2
Soms heeft zo’n figuur een mooie vorm met gelijke zijden. Bijvoorbeeld: een rechthoek. Bij een rechthoek bereken je de omtrek door: 2x de lengte en 2x de breedte (of: lengte + breedte + lengte + breedte)!!
Afspraak 3
Een nóg mooier figuur is het vierkant. Deze heeft vier gelijke zijden. Wanneer je dus de lengte van een zijde weet, weet je genoeg. Bereken de omtrek van een vierkant door: 4x de lengte.
Oppervlakte
Wanneer ik de oppervlakte van een figuur wil berekenen, moet ik kijken naar wat zich binnen de lijnen van een figuur bevindt. Bij onregelmatige figuren is het vaak moeilijk om precies aan te geven hoeveel de oppervlakte is. Er wordt dan vaak gewerkt met schatten.
Afspraak 1
Bij ‘mooie’ figuren zoals bijvoorbeeld rechthoeken bereken je de oppervlakte door: lengte x breedte.
Afspraak 2
Het antwoord geef ik altijd in ‘vierkante’ (meter, decimeter, centimeter, enz.).
Afspraak 3
Dit ‘vierkante’ geef ik aan door er een 2 bij te zetten (m2, dm2, cm2, mm2, enz.).
Let op!!!
| 1 HECTARE = 1 vierkante hm (hm2) 1 ARE = 1 vierkante dam (dam2) 1 CENTIARE = 1 vierkante m (m2) |
Inhoud
Wanneer ik de inhoud moet berekenen, wil ik weten hoeveel ergens in kan en hoeveel ergens in zit. Bijvoorbeeld: hoeveel water zit er in dat zwembad?
Afspraak 1
Inhoud bereken ik door: lengte x breedte x hoogte
Afspraak 2
Het antwoord geef ik aan met ‘kubieke’ (meter, decimeter, centimeter, enz.).
Afspraak 3
1 liter is hetzelfde als 1 kubieke dm.
| 1 LITER = 1 KUBIEKE DECIMETER (dm3) |
Priemgetallen
Dit zijn getallen die alleen deelbaar zijn door het getal 1 en zichzelf!!! 17 is bijvoorbeeld een priemgetal, omdat je 17 alleen kunt delen door 1 en door 17. Het getal 1 is zelf geen priemgetal.
Romeinse cijfers
De Romeinen gebruikten de volgende cijfers:
I = 1
V = 5
X = 10
L = 50
C = 100
D = 500
M = 1000
Afspraak 1
Wanneer er meerdere ‘cijfers’ in een Romeins getal voorkomen, moet je ze altijd lezen van groot naar klein. Begin dus altijd met het cijfer met de grootste waarde.
Afspraak 2
Een cijfer met een kleinere waarde dat VÓÓR een cijfer met een grotere waarde staat, TREK JE ERAF! Bijvoorbeeld: CM = 1000 – 100 = 900. Staat het cijfer ERACHTER, dan TEL je de waarde ERBIJ OP! Bijvoorbeeld: MC = 1000 + 100 = 1100.
Afspraak 3
Wanneer een cijfer meer dan één keer voorkomt, tel je het aantal keren en de waarde ervan. Bijvoorbeeld: MCCC = 1000 + 3 x 100 = 1300.
Tijd
1 etmaal = 24 uur (dag en een nacht)
1 uur = 60 minuten, 4 kwartier of 3600 seconden
1 kwartier = 15 minuten
1 minuut = 60 seconden
De KORTE WIJZER geeft altijd de UREN aan.
De LANGE WIJZER geeft altijd de MINUTEN aan.
Digitale tijd
Zoals je weet, kan de tijd ook aangegeven worden met cijferts. Let hierbij op de volgende afspraken:
Afspraak 1
De cijfers VOOR de dubbele punt (:) geven de UREN aan. Dit kunnen de cijfers 1 t/m 23 zijn.
Afspraak 2
De cijfers NA de dubbele punt geven de MINUTEN aan. Dit kunnen de cijfers 1 t/m 59 zijn.
Afspraak 3
Van 0:00 tot 12:00 is van middernacht tot 12 uur ’s middags.
Afspraak 4
Van 12:00 tot 0:00 is van ’s middags to0t middernacht.
Afspraak 5
Bij het lezen van een digitale tijd is het nodig om aan te geven of het 3 uur ’s nachts of ’s middags is!!
3 uur ’s nachts wordt aangegeven met: 3:00
3 uur ’s middags wordt aangegeven met: 15:00
Afspraak 6
Moet je een tijd lezen die ‘groter’ is dan 12 uur, trek er dan voor het gemak 12 uren van af!
Bijvoorbeeld: 16:30 (16 – 12 = 4) is 4 uur + 30 minuten ’s middags, oftewel half vijf.
Rekenweetjes
Wat bedoelen ze ook alweer met:
de SOM: de uitkomst van een + of ERBIJsom
het VERSCHIL: de uitkomst van een ERAFsom
het PRODUKT: de uitkomst van een x of KEERsom
het QUOTIËNT: de uitkomst van een : of DEELsom
